Before beginning this section, make sure that you are comfortable with the rules of order of operation in mathematical equations. It is necessary to know in what order you add, subtract, divide and multiply in an equation.
Algebraic equations involve using letters and symbols to represent unknown numbers. In order to solve these equations you must isolate the unknown variable. We will begin with a couple of simple examples.
When solving algebraic equations, it is important to know the opposite mathematical operations. For example, subtraction is the opposite of addition and division is the opposite of multiplication. Square roots are the opposite of squaring. We will not cover square roots in this section.
Example 1
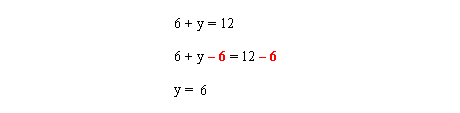
In order to isolate the “y” eliminate a + 6 on the left hand side of the equation. In algebraic equations whatever you do to one side of the equation, you also have to do to the other side. Subtract 6 from both sides.
Example 2
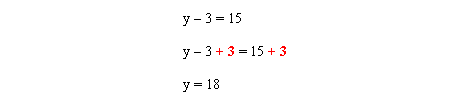
In order to isolate the “y”, eliminate a - 3 on the left hand side of the equation. Add 3 to both sides.
Example 3
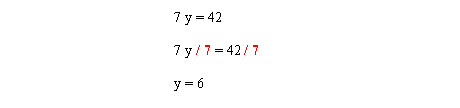
In this case “y” is multiplied by 7. To eliminate a number that is being multiplied divide by the same number. Divide both sides by 7.
Example 4
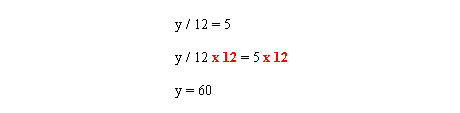
In this case “y” is divided by 12. To eliminate a number that is being divided, multiply by the same number. Multiply both sides by 12.
Sample Questions
Practice solving some of these simple equations. Answers are below.
1) y / 11 = 23
2) 15 + y = 63
3) – 5 + y = 10
4) 13 (y) = 130
5) 5 y = 15
6) 6 + 3 + y = 56
7) 2(y) = 56
8) y / 8 = 4
9) y (24) = 72
More Advaned Algebraic Equations
When solving equations, follow the order of operations, which dictate that you perform equations within brackets, followed by exponents, then division and multiplication, and finally addition and subtraction. When isolating unknown variables, use the opposite order. We will not cover solving equations with exponents at this level.
Example 5
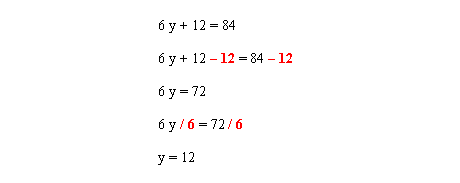
In order to isolate the “y” first eliminate a + 12 on the left hand side of the equation. Subtract 12 from both sides. You are left with 6y = 72. To isolate “y”, now simply divide both sides of the equation by 6.
Example 6

You may encounter equations where one side has operations without an unknown variable. In cases like this, solve the side without an unknown variable FOLLOWING THE STANDARD ORDER OF OPERATION RULES.
After you have accomplished this, solve the equation in the standard manner. People more advanced in math will be able to consolidate portions of the left side as well, but unless you are comfortable you should proceed the way outlined to the left.
Example 7
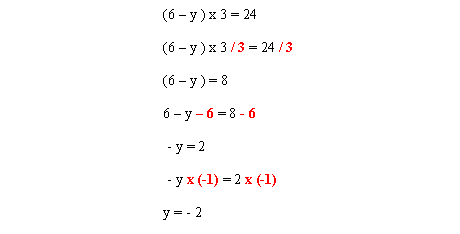
Perform this equation following the standard rules. Leave the brackets until the end. When only the brackets remain, you can get rid of them, as they no longer serve a purpose.
When you are left with an equation where the unknown is isolated, but negative, simply multiply both sides of the equation by – 1 to inverse the signs.
The end result is that y = - 2.
Example 8
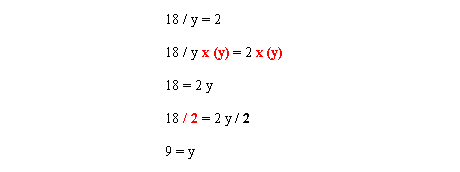
One other tricky situation you may encounter is when “y” appears on the bottom of a division equation. In order to solve for “y”, move it from the bottom of the division sign by multiplying both sides of the equation by “y”. The result is 18 = 2 y. Now solve the rest of the equation.

More Sample Questions
a) 3 (y) + 6 – 10 = 89
b) (y) / 6 + 24 – 2 = 14
c) - y (3) +55 = 105
d) 5 y – 32 = 24 (3)
e) –32 + 6y/2 = 64
f) 22 y + 16 (8) = 6 y
Answers
1) 253
2) 48
3) 15
4) 10
5) 3
6) 47
7) 28
8) 32
9) 3
a) 31
b) - 48
c) –16.7
d) 20.8
e) 32
f) – 8







